Structure Of
Flame Balls At Low Lewis-number (SOFBALL):
Preliminary Results from the STS-83 and STS-94 Space Flight
Experiments
Paul D. Ronney,
Ming-Shin Wu and Howard G. Pearlman
Department of Aerospace and Mechanical Engineering
University of Southern California, Los Angeles, CA 90089
Karen J. Weiland
Microgravity Science Division
NASA Lewis Research Center, Cleveland, OH 44135
ABSTRACT
Results from the Structure Of
Flame Balls At Low Lewis-number (SOFBALL) space flight experiment
conducted on the MSL-1 Space Shuttle missions are reported.
Several new insights were obtained, including: much lower
buoyancy-induced drift speed than anticipated pre-flight;
repulsion of adjacent flame balls due to their mutual
interaction; remarkable sensitivity of flame balls to small
accelerations resulting from Orbiter attitude control maneuvers;
and very similar net heat release for all flame balls in all
mixtures tested. Comparison of experimental results to
computational predictions reveals limitations in current models
of H2-O2 chemistry for very lean mixtures.
It is discussed how the results of these space experiments may
provide an improved understanding of the interactions of the two
most important phenomena in combusting materials, namely chemical
reaction and transport processes, in the unequivocally simplest
possible configuration.
INTRODUCTION
Flames are typically classified
as "premixed" flames, where all reactants (for example
fuel and air) are intimately mixed on the molecular level before
the combustion process is started, and "nonpremixed" or
"diffusion" flames, where the fuel and oxidant must mix
before combustion can take place. Premixed flames include the
familiar laboratory Bunsen burner as well as the flames inside of
a gasoline-fueled internal combustion engine. It is well known
that premixed gas flames containing too little fuel ("lean
mixtures") or too much fuel ("rich mixtures") will
not burn. Despite many years of study, these lean and rich
"flammability limits" and the behavior of weakly
burning flames near these limits are not well understood. For
example, the best available predictions of the burning velocities
of very lean hydrogen-air mixtures near flammability limits are
higher than the experimental measurements by a factor of 2 (Ref.
1). Away from these limits, the agreement between model and
experiment is much more satisfactory. Understanding combustion
under lean conditions is critical to the design of efficient,
clean-burning combustion engines. Lean-burning hydrogen-fueled
engines are frequently considered as a means of meeting
California's upcoming ultralow emission vehicle standards and the
proposed federal emission standards for beyond the year 2000.
Also, knowledge of near-limit behavior of flames is necessary for
the assessment of fire and explosion hazards in mine shafts, oil
refineries and chemical plants2.
It has been known for many
years2 that most near-limit phenomena are influenced
by gravity through the effects of buoyant convection on the
transport rates of thermal energy and reactants to/from the
chemical reaction zones. This has motivated a number of recent
experiments on flame propagation in a µg environment3,4.
It has been found that in a µg environment the absence of
buoyant convection emphasizes other transport mechanisms,
including the unequal rates of diffusion of thermal energy and
diffusion of molecular reactants (the Lewis number effect) and
the spectral radiation emitted from the gaseous combustion
products. As a consequence of the change in the relative
magnitudes of various transport mechanisms at µg, a number of
new near-limit phenomena have been observed. Perhaps the most
unusual of these are "flame balls," which are the
subject of the SOFBALL flight experiment.
SCIENTIFIC
BACKGROUND
Over 50 years ago, Zeldovich5
showed that the steady heat and mass conservation equations admit
a solution corresponding to a stationary spherical flame
or "flame ball" (Fig. 1), just as the same governing
equations in planar geometry admit a steadily propagating flame
as a solution for every mixture. In the former case the solutions
are characterized by a radius (r*) and in the latter
case by the burning velocity. The mass conservation equation in a
steady spherically symmetric system with no sources or sinks, —.(ru) = 0,
where r is the density and u the fluid velocity
vector, requires that u be identically zero everywhere. In
spherical geometry, the solution to steady, convection free
diffusion equations for temperature and chemical species, —2T = 0 and —2Y,
where T is the temperature and Y the fuel mass fraction, are of
the form c1 + c2/r, where r is the radial
coordinate and c1 and c2 are constants.
This form satisfies the requirement that T and Y be bounded as r Æ
. For cylindrical and planar geometry the corresponding
forms are c1 + c2ln(r) and c1 +
c2r, respectively, which are obviously unbounded as r Æ
. For this reason theory admits steady flame ball
solutions, but not "flame cylinder" or "flame
slab" solutions. Zeldovich showed that for an adiabatic
flame ball, the energy and species conservation equations could
be combined to infer the temperature at the surface of the flame
ball (T*):
T* =
T + (Tad - T)/Le (1),
where T is the ambient
temperature, Tad the adiabatic flame temperature and
Le the Lewis number, defined as ratio of the mixture thermal
diffusivity (a) to the mass diffusivity (D) of the
stoichiometrically limiting reactant (which is always the fuel
for the purposes of the discussion here.) Thus, the temperature
profile is given by T(r) = T + (T* - T)r*/r,
where r* is the flame ball radius. Zeldovich also
showed that flame ball solutions are unstable and thus probably
would not be physically observable, just as planar flames are
frequently subject to instabilities which prevent them from
remaining planar.
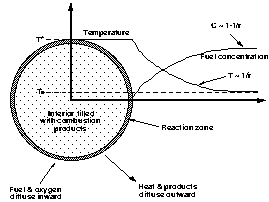
|
|
| Figure 1. Schematic diagram of a
flame ball, illustrated for the case of fuel-limited
combustion at the reaction zone. The oxygen profile is
similar to the fuel profile except its concentration is
non-zero in the interior of the ball. The combustion
product profile is identical to the temperature profile
except for a scale factor. |
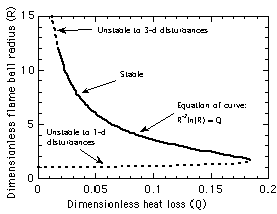
Figure 2. Theoretical prediction8
of the effect of heat loss on flame ball radius and
stability properties with single-step Arrhenius
chemistry, constant thermodynamic and transport
properties and volumetric heat loss from the interior of
the ball. |
Forty years later after
Zeldovich’s analysis, seemingly stable flame balls were
accidentally discovered in drop-tower experiments6 in
lean hydrogen-air mixtures (Le š 0.3) and subsequently
observed in drop-tower and aircraft experiments7 in H2-O2-CO2
(Le š 0.2), H2-O2-SF6 (Le
š 0.06) and CH4-O2-SF6
mixtures (Le š 0.3). The µg environment of the drop tower
was needed to obtain spherical symmetry and to avoid
buoyancy-induced extinction of the flame balls. The following
sequence of phenomena was observed as the mixtures were
progressively weakened by addition of air, inert gas or chemical
inhibitor. For mixtures sufficiently far from flammability
limits, flame balls consistently split into more flame balls,
resulting in an expanding spherical front composed of many
individual cells, similar to the cellular fronts resulting from
the diffusive-thermal instability widely observed at 1g in
mixtures with low Le. For weaker mixtures closer to the
flammability limits, stable flame balls were observed. For still
weaker mixtures all flames extinguished. It was concluded that
flame balls would probably occur in all combustible mixtures with
low Le for mixtures close to the extinction limits, however, the
short duration of drop tower experiments and the substantial
fluctuations in the acceleration level in aircraft µg
experiments precluded definite conclusions.
These results were found to be
qualitatively the same over the range 0.06 < Le < 0.3, with
H2 and CH4 fuels, with or without added CF3Br
(a chemical inhibitor) and at pressures from 0.5 to 3 atm,
indicating that variations in Lewis number over this range,
chemical mechanisms, and radiation spectra do not qualitatively
influence these phenomena.
The apparent discovery of
stable flame balls motivated a search for a stabilizing
mechanism. Zeldovich5 had noted the possibility of
heat losses stabilizing flame balls. The effects of volumetric
radiative losses (e.g., due to gas radiation) on flame
balls were analyzed by Buckmaster and collaborators8,9.
When the heat losses are not too strong, two stationary flame
ball radii are predicted (Fig. 2), a "large" flame ball
that is strongly affected by heat loss and a "small"
flame ball that is nearly adiabatic, and when the losses are
sufficiently strong no solutions exist, indicating a flammability
limit. As the limit is approached, the difference between the
radii of the "large" and "small" balls
decreases to zero. Stability analyses8.9 showed that
all small flame balls are unstable to radial disturbances, i.e.,
the flame will either grow outward from the equilibrium radius
(and possibly develop into a propagating flame) or collapse
inward and extinguish. The basic reason is that as the flame ball
radius increases, the surface area to volume ratio decreases,
thus the ratio of total heat release (which is proportional to
the flame ball surface area) to total radiative heat loss (which
is proportional to the flame ball volume) increases, thus the
flame ball becomes weaker and shrinks. Conversely, if the radius
decreases, the flame ball grows stronger and expands. Thus, flame
balls with sufficient volumetric losses can be stable to radial
disturbances. Large flame balls with weak heat loss effects, i.e.,
far from the flammability limits, are predicted8,9
unstable to three-dimensional disturbances, which is consistent
with the observation of splitting cellular flames in these
mixtures. Consequently, a portion of the large flame branch close
to the extinction limits is stable to both types of disturbances,
which is consistent with the experimental observations.
It has also been predicted10
that stable flame balls can only exist for mixtures with mixtures
having Le less than a critical value which is less than unity,
which explains why flame balls are not observed for mixtures with
Le less than but close to unity (e.g. CH4-air)
or larger than unity (e.g. C3H8-air),
even for near-limit mixtures at µg. Instead, conventional
propagating flames are observed under these conditions.
Flame balls have several unique
and interesting properties which indicate a number of practical
applications. Since they are one-dimensional, steady and
convection-free, they are the simplest possible type of premixed
flame structure and therefore provide a useful test-bed for
theoretical and numerical models of the interaction between
chemical and transport processes in flames, especially near
flammability limits. Some of these interactions are not predicted
well even by the best currently available models. For example,
numerical simulations of flame ball properties11,13
employing detailed chemical, radiation and transport models in a
spherically symmetric system show that different published
chemical reaction models for hydrogen-oxygen oxidation predict
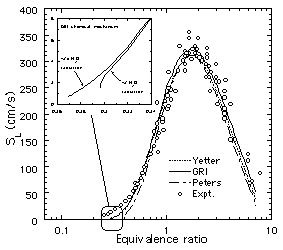
widely varying flame ball characteristics (Fig. 3), even though
all of these models can accurately predict the burning velocities
of flames in hydrogen-air mixtures farther away from the
extinction limits (Fig. 4). This is particularly significant
because models of hydrocarbon combustion chemistry must have an
accurate H2-O2 sub-mechanism if they are to
be able to model hydrocarbons accurately. Also, since flame balls
can be observed in mixtures that are well outside the
conventionally defined extinction limits, microgravity can be a
more hazardous environment from the point of view of fire safety.
Flame balls warrant particular concern because they do not
propagate; this makes fire detection and suppression more
difficult. This potential problem is compounded because hydrogen
burns without visible radiation or smoke, and because sources of
hydrogen abound on spacecraft (e.g., in propulsion and
fuel cell systems). Flame balls may also be relevant to the
turbulent combustion of mixtures with low Lewis number because
flame balls are more robust than plane flames (the computed11
radiation-induced extinction limit of flame balls in lean H2-air
mixtures is 3.43% H2, whereas for plane flames it is
11.1%.) Consequently, sufficiently strong turbulence may
extinguish planar flames, whereas flame balls could persist under
the same conditions. Hence, structures reminiscent of flame balls
could be the prevalent ones in near-limit turbulent combustion of
lean hydrogen-air mixtures in engines.
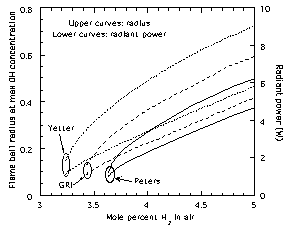
|
|
| Figure 3. Predicted13
steady flame ball radii and radiant emission in H2-air
mixtures using the GRI17,
Peters18 and Yetter19
chemical models. |
Figure 4. Predicted13
steady burning velocities (SL)
of H2-air mixtures using the
GRI17, Peters18
and Yetter19 chemical
models. A compilation20 of
experimental results from several sources is also shown. |
EXPERIMENTAL
APPROACH
Based on the above discussion,
the objectives of the SOFBALL experiment can be summarized as
follows:
• Determine whether
steady, stationary flame balls can exist in an
extended-duration µg environment
• Assess the influence of gaseous radiation on flame
ball size and stability
• Determine whether flame ball motion (if observed) is
due to the non-zero gravity level (present to a small extent
even in the Spacelab environment)
• Determine the effect of Lewis number and radiation on
flame balls through the use of mixtures employing different
diluent gases
The drop-tower and aircraft µg
experiments indicate that a very long duration and high quality
µg environment is necessary to assess the steady properties and
stability limits of flame balls. A theoretical estimate of the
time required can be made in the following way. The response time
of flame balls is on the order of the time for thermal diffusion
of energy from the near-field region of the flame ball to the
far-field region. Theory8,9 shows that the former
region is characterized by radii of the order of r*
and the latter region is characterized by radii of the order of qr*,
where q º E/RT* is the non-dimensional activation
energy, E the dimensional overall activation energy of the heat
release reactions and R the gas constant. Consequently, the
far-field time scale is of the order (qr*)2/a.
Since typical values of r*, q and a
are 5 mm, 10 and 20 mm2/s, respectively, for lean H2-air
mixtures, a representative time scale for flame ball evolution is
125 s - much longer than the time available from drop-tower or
aircraft facilities. This evolution time scale is confirmed by
numerical simulations11,13. Another consideration is
that the gravity level must be small enough that the flame balls
are not significantly affected by convection. The drift velocity
of flame balls based on aircraft µg data was found7
to be 1.5(gr*)1/2, where g is the
gravitational acceleration. Since velocities on the order of a/r*
are sufficient to disturb flame balls12,
g << 1.5 x 10-4 go,
where go is earth gravity, is required to obtain
diffusion-dominated flame balls (as opposed to
convection-dominated flames.) To insure that the conductive flux,
represented by a/r*, is significantly less
than the convective flux, represented by the drift velocity, the
acceleration level should be a factor of q less than
this, or 1.5 x 10-5 go. Another requirement is that the
acceleration is small enough that the flame balls do not drift
into the walls of the combustion chamber before at least one
characteristic evolution time has elapsed. This coincidentally
also requires a gravity level of 1.5 x 10-5 go
or lower in the combustion chamber employed, which has a radius
of 160 mm. This required time and quality of µg indicate the
need for space experiments. The SOFBALL experiment on MSL-1
provided the requisite µg environment.
The SOFBALL experiments were
performed in the Combustion Module-1 facility, developed by the
NASA-Lewis Research Center in Cleveland, Ohio. A cylindrical
chamber of 320 mm inside diameter and 320 mm length was filled
from one of 14 bottles containing a pre-specified weakly
combustible H2-air, H2-O2-CO2
or H2-O2-SF6 gas mixture and
ignited using electric sparks of variable deposited energy up to
700 mJ with spark gaps variable from 0.35 to 10 mm. The optimal
energy and gap were determined pre-flight by aircraft µg tests.
The flame balls evolving from this ignition source were observed
using two intensified video cameras (sensitive to visible and
near-IR emissions from 400 to 900 nm) with orthogonal views, a
set of six thermocouples to measure gas temperature, and four
radiometers (two unfiltered and two with a 5 µm - 7.5 µm
band-pass filter to detect only H2O radiation) to
measure the radiant heat flux emitted from the flames.
Additionally, the chamber pressure was recorded during the test
and the pre- and post-combustion gas compositions were measured
using a gas chromatograph. The on-orbit acceleration levels were
measured by the four different on-board accelerometer systems
(OARE, MMA, SAMS and QSAM). The PI Microgravity Services (PIMS)
team provided the SOFBALL team with OARE acceleration data
transformed to the combustion chamber location; the accelerations
reported below use these specially processed data.
EXPERIMENTAL
RESULTS
Two of the fifteen scheduled
SOFBALL experiments were successfully conducted during the
shortened STS-83 mission. A total of seventeen test points were
performed on STS-94, including all fifteen planned combustion
tests plus two additional tests (obtained by creating gas
mixtures from bottle residuals), of which sixteen of these
seventeen mixtures ignited. These mixtures tested on STS-83 and
STS-94 produced from one to nine flame balls, with the mixtures
having more fuel producing multiple flame balls. Most of the
tests burned for 500 seconds, until the experiment timed out and
a mixing fan extinguished the flames. As discussed later, it had
not been expected that any flame balls would last this long.
Unfortunately, it was not possible to change the experiment
duration after the STS-83 mission but before the STS-94 mission,
mostly due to the time that would have been required to re-verify
the control software. Ten of the mixtures from STS-94 were
ignited a second time (since there was ample remaining fuel in
many cases) and eight of these burned for an additional 500
seconds.
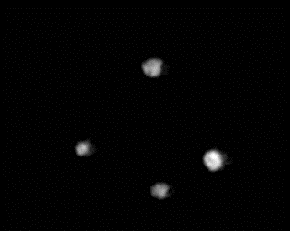
A typical image of the flame
balls is observed in H2-air mixtures is shown in Fig.
5. For this and most of the H2-air tests, unlike most
H2-O2-CO2 and H2-O2-SF6
tests, all flame balls extinguished before the 500 s experiment
time-out. This is mainly because the flame balls are larger in H2-air
mixtures and the fuel (hydrogen) diffusivity is higher in N2
than in CO2 or SF6. Both of these factors
led to more volume of fuel being consumed per unit time in H2-air
tests for the same number of flame balls.
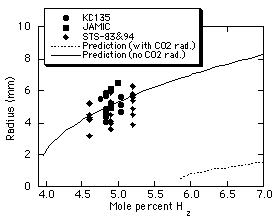
Figure 6 shows measured flame
ball radii for H2-air mixtures as a function of the
fuel concentration. The radius is arbitrarily defined as the
half-width of the flame ball intensity profile and one-third of
the maximum intensity. Data obtained in the space experiments is
very consistent with data obtained in the 10-second drop tower at
the Japan Microgravity Center (JAMIC)21 as well as
recent aircraft21 tests. (Other properties, notably
temperature profiles and radiative emission, are very different
in the drop tower, aircraft and space experiments.) The flame
ball radii are in poor agreement with our computational
predictions, mainly because of uncertainties in the chemical
reaction rates (Fig. 3), and in fact none of the mechanisms
predict radii in agreement with experimental observations.
|
 |
| Figure 5. Image of flame balls
obtained in 3.85% H2 / 96.15% air mixture, taken 25 s
after ignition. Field of view is 112 mm x 150 mm. |
Figure 6. Predicted13
flame ball radii in H2-air
mixtures along with measured flame ball radii from
aircraft µg experiments21,
JAMIC drop-tower experiments21,
and the STS-83/94 space experiments. |
A typical image of the flame
balls is observed in H2-O2-CO2
mixtures is shown in Fig. 7. The flame balls drifted several tens
of mm away from each other during this test, but the imaginary
point at the "center of mass" of the three balls hardly
moved at all during the 500 s test period. Thus, the flame ball
movement is likely due to an interaction of the balls rather than
buoyancy-induced drift. Both of these mechanisms of flame ball
drift are discussed in the following section.
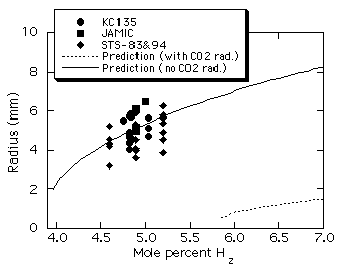
Figure 8 shows measured flame
ball radii for H2-O2-CO2
mixtures as a function of the fuel concentration. Again, data
obtained in the space experiments is very consistent with data
obtained in the JAMIC and aircraft tests. Note that our numerical
model13 predicts that no mixtures below 5.8% H2
are flammable, and even for 5.8% H2 and higher, the
predicted flame ball radii are much smaller than those observed
in drop tower and aircraft µg experiments. The discrepancies are
believed to be due to the effect of reabsorption of emitted
radiation by the CO2 diluent gas, which is neglected
in current models11,13. Reabsorption is expected to be
important for the CO2-diluted mixture because the
Planck mean absorption length (LP) for CO2
at 1 atm and 300K is 42 mm, which is much smaller than the radius
of the combustion chamber. These effects are also important for
the H2-O2-SF6 mixtures (LP
š 3.5 mm) but not for H2-air mixtures, where the
only radiating specie is the product H2O where LP
š 1 m. Consequently, for H2-O2-CO2
and H2-O2-SF6 mixtures much of
the radiation emitted from within or near the flame ball will not
be lost to the chamber walls but instead will be reabsorbed
within the gas. An approximate theoretical model of flame balls
including radiative reabsorption effects14 predicts
that as the absorption length scale decreases, the flame ball
size increases and the flammability limit shifts to weaker
mixtures, which is consistent with the observed discrepancies. A
computational estimate of an upper bound for reabsorption
effects in H2-O2-CO2 mixtures
was obtained13 by artificially neglecting CO2
radiation entirely in the numerical model, which is equivalent to
assuming zero absorption length. Figure 8 shows that the actual
flame ball radii are much closer to that predicted assuming this
upper bound for reabsorption effects rather than that predicted
without reabsorption.
 |
 |
| Figure 7. Image of flame obtained in
4.9% H2 / 9.8% O2 / 85.3% CO2 mixture, taken 130 s after
ignition. Field of view is 112 mm x 150 mm. |
Figure 8. Predicted13
flame ball radii in H2-O2-CO2
mixtures (H2:O2
= 1:2) including and excluding CO2
radiation, along with measured flame ball radii from
aircraft µg experiments21,
JAMIC drop-tower experiments21,
and the STS-83/94 space experiments. |
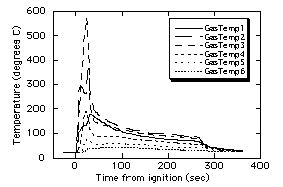
The gas temperature data
obtained from the H2-air test shown in Fig. 5 are
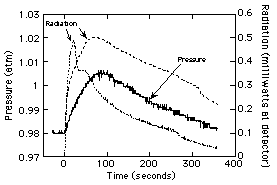
given in Fig. 9, and the chamber pressure and radiometer data are
given in Fig. 10. These data are much more dynamic than that from
the previous test, which is expected since 5 balls of varying
size were observed and all extinguished at varying times during
the test. The maximum temperature observed was 576ûC, which
compares to the maximum predicted13 temperature of
862ûC. This discrepancy is not surprising considering that no
flame ball was observed to make a "direct hit" on a
thermocouple junction.
 |
|
| Figure 9. Measured gas temperatures
for Test #2. Thermocouple locations corresponding to
GasTemp1 through GasTemp6 are 30, 50, 70, 90, 110 and 130
mm from spark gap, respectively. |
Figure 10. Measured chamber pressure
and radiant emissions for Test #2. |
DISCUSSION
Buoyancy-induced flame ball
drift
It had not been expected that
the flame balls would last more than about half of the 500 s
experiment time-out period because the drift velocity (v) of
flame balls was expected to be given by the formula7
v š 1.5 (2).
(2).
This empirical relation was
inferred from data on drift velocity obtained in KC-135 µg
aircraft experiments, where accelerations are on the order of 10-2
go. According to Eq. (2), even at 1 µg, a flame ball
with radius 3 mm will drift 129 mm, nearly the radius of the
chamber, in 500 s. The form of Eq. (2), v ~  , is that of a bubble rising in an
inviscid fluid15, which implies viscosity effects are
negligible. This is reasonable for the conditions in the aircraft
experiments, where 50 is a typical Reynolds number (Re) based on
the observed g-induced drift velocity and the "equivalent
buoyant radius" of the flame ball, inferred to be about five
times the visible radius7. (The high-temperature, low
density region of the flame ball extends far beyond the visible
radius, as implied by Fig. 1, thus the volume of buoyant gas is
much larger than the volume of the flame ball itself.) In
contrast, at 1 µg, Re will be much less than unity and the
viscous, creeping-flow relation for bubbles15
, is that of a bubble rising in an
inviscid fluid15, which implies viscosity effects are
negligible. This is reasonable for the conditions in the aircraft
experiments, where 50 is a typical Reynolds number (Re) based on
the observed g-induced drift velocity and the "equivalent
buoyant radius" of the flame ball, inferred to be about five
times the visible radius7. (The high-temperature, low
density region of the flame ball extends far beyond the visible
radius, as implied by Fig. 1, thus the volume of buoyant gas is
much larger than the volume of the flame ball itself.) In
contrast, at 1 µg, Re will be much less than unity and the
viscous, creeping-flow relation for bubbles15
 (3),
(3),
where the b subscript refers to
the bubble properties, should be employed instead of Eq. (2).
Modeling the flame ball as a bubble whose radius is the
equivalent buoyant radius (= 5r*) mentioned above and
using temperature-averaging of gas properties based on a maximum
temperature of 1200K, Eq. (3) becomes
 (4).
(4).
While the validity of Eq. (4)
has not yet been confirmed, this appears to be an example of
circumstances where ground-based µg experiments led to
inaccurate predictions of the behavior of a space experiment.
With very low drift velocities,
it is possible that in many cases the flame balls could continue
to burn until their fuel supply has been depleted sufficiently
that the remaining mixture was no longer flammable, rather than
drifting into the chamber wall first. In a few of the Estimates
for the maximum possible burn duration developed based on
mechanism suggest that in the 3 atm H2-O2-SF6
mixtures which produced only one flame ball, the ball could burn
for about 17 hours!
Flame ball mutual repulsion
It was found that in both tests
the flame balls drifted apart from each other throughout the
duration of the burn. This had been seen in drop tower tests, but
the test durations had been too short to obtain meaningful data
on separation rates. In the space experiments it was found that
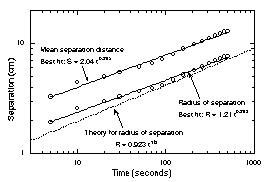
the drift rate continually decreased with time. Figure 11 shows
the mean separation between the three flame balls seen in Fig. 7
as a function of time, and the mean radius of separation,
determined by finding the radius of the circle passing through
all three flame ball centers. The camera view (not shown)
orthogonal to that seen in Fig. 7 shows three practically
collinear balls, which indicates that in the view shown in Fig.
7, the plane of the flame balls is orthogonal to the axis of the
camera lens, which in turn indicates that the measure of flame
spacing seen in this view is a reasonably accurate indication of
the true spacing.
A proposed mechanism of flame
ball drift based on the mutual depletion of total enthalpy
(chemical plus thermal) by two flame balls in the region between
them is presented here. When two flame balls are in close
proximity, they have two influences on each other: first, they
deplete each other of reactants from the region between them
(decreased chemical enthalpy) and two, they increase the
temperature in the region between them (increased thermal
enthalpy). Because of the enthalpy gradient, one side of the
flame ball will have a temperature slightly greater than T*
while the other will be slightly lower, thus leading to
differences in heat release rate on the two sides of the ball. It
is proposed that the ball must drift in the direction of
increasing total enthalpy at a rate whereby the convective
transport of enthalpy to the ball balances this difference in
heat release rate. A model of flame ball drift has been
developed, resulting in the prediction16
 (5).
(5).
The prediction of Eq. (5) with
the representative parameters for Test #1 (T* š
1200K, To = 300K, ao š 10 mm2/s,
r* = 3 mm, Le = 0.2) are shown in Fig. 11, where the
formula has been multiplied to by (8/3)1/3 to
account for the additional gradient caused by presence of three
rather than two flame balls as well as transformation of the
prediction from mean spacing to mean radius of separation. The
agreement between theory and experiment is fairly close, and so
may indicate some validity for the proposed mechanism.
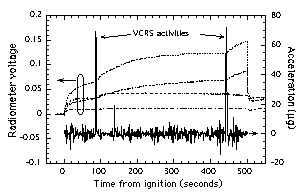
The flame balls were found to
be much more sensitive to Orbiter Vernier Reaction Control System
(VRCS) thruster firings than expected pre-flight. These firings
produced a noticeable change in the flame ball position, drift
speed, and especially radiometer data (Fig. 12). The strong
effect of microgravity disturbances on radiation is probably due
to the fact that the visible flame ball is surrounded by a much
larger volume of hot but non-reacting gas. Most of the radiation
is emitted from this large gas volume rather than from within the
flame ball itself11. This large ball of gas is
extremely susceptible to buoyancy-induced motion resulting from
even the smallest VRCS impulses (on the order of 50 µg for 1 sec
= 0.5 mm/sec). (Careful inspection of the two data sets from
STS-83 also showed this trend, but it was much less noticeable in
these cases because both STS-83 tests produced multiple flame
balls with more widely dispersed hot gas regions that, as a
group, are much less affected by the VRCS firings than tests
producing only one or two flame balls.) Note that Fig. 12 shows
that only VRCS firings, which cause a net change in the Orbiter
momentum, had any effect; vibrations resulting from crew and
Orbiter systems operations, which do not affect the net momentum
of the Orbiter, had practically no effect. Once the effects of
the VRCS firings were seen, "free drift" (suppression
of VRCS firings) was requested during the remaining experiments
and was granted in many cases. When free drift could be
maintained for the entire test period, the disturbances to the
radiometer readings did not occur.
|
|
| Figure 11. Observed radius of separation
and mean separation of the three flame balls seen in Fig.
7 as a function of time, and comparison to theoretical
predictions16. |
Figure 12. Example correlation of
radiometer readings with Orbiter acceleration environment
during STS-94 mission showing impact of VRCS thruster
firings. For clarity, only the Orbiter z-axis (vertical)
acceleration component is shown. Mixture: 6.50% H2
- 13.00% O2 - 80.50% SF6, 1 atm
initial pressure. |
Preliminary inspection of the
flight data suggest that the flame balls respond ballistically to
the VRCS impulses, that is, the impulse (change in velocity)
imparted to the ball is the same as the acceleration impulse.
This change in velocity then decays on a time scale of tens to
hundreds of seconds, comparable to the viscous time scale
associated with the flame ball and its surrounding hot gas field.
SUMMARY AND
CONCLUSIONS
Two space-based experiments on
STS-83 and 24 experiments on STS-94 have shown that flame balls
are in fact stable for very long periods of time in a µg
environment. The rate at which the flame balls drift due to the
small acceleration levels on the spacecraft was far smaller than
that expected before the mission. A modified mechanism of
buoyancy-induced drift is proposed based on the difference
between the flow regimes in the aircraft and space experiments
(nearly inviscid flow vs. creeping flow), and a new mechanism of
flame ball drift induced by mutual interaction of adjacent flame
balls is proposed. Flame ball properties, especially radiative
emission, were found to be strongly affected by orbiter Vernier
Reaction Control System thruster firings. This may have important
implications for combustion experiments to be performed on the
International Space Station.
Another finding of these
experiments is that the differences between computer models and
experiments found based on earlier short-duration µg tests were
also found in the space experiments. Different models of H2-O2
chemistry yield different predictions for flame ball properties,
and it is expected that detailed evaluation of the results of the
space experiments will help lead to the identification of the
most appropriate chemical models for lean-limit combustion of
hydrogen and hydrocarbon fuels.
A reflight of the SOFBALL
experiment is planned for STS-107 in the fall of 2000. Among the
changes planned for SOFBALL-2 include longer test durations,
since most flame balls were still burning at the end of the 500 s
tests on STS-83 and STS-94. A third intensified video camera with
a smaller field of view but greater spatial resolution will be
added. A higher energy ignition system will be used to study
still-leaner mixtures, particularly in the H2-air
family. Optical filters will be used on some of the intensified
video cameras in order to determine if the emission wavelength
has an impact on the apparent flame ball sizes.
ACKNOWLEDGMENTS
The authors wish to thank the
CM-1 Project Managers, Mr. Roy Hager (retired) and Ms. Ann Over,
the CM-1 Project Engineer, Mr. Ron Chucksa (retired) and the
entire CM-1 engineering and operations team for their tremendous
effort in designing, constructing, testing and operating the CM-1
facility. Angel Abbud-Madrid, Mohammed Abid, Quin Blackburn and
Jian-Bang Liu assisted with the data analysis during and after
the missions. Special thanks is owed to the STS-83/94 crew for
conducting the experiments, and the MSFC mission management team,
led by Ms. Teresa Vanhooser and Dr. Michael Robinson, for
coordinating experiment operations. This work was supported by
NASA grants NAG3-1242, NAG3-1523 and NAG3-2124.
REFERENCES
1Eolfopoulos, F. N.
and Law, C. K., "An Experimental and Computational Study of
the Burning Rates of Ultra-lean to Moderately-rich H2/O2/N2
Laminar Flames with Pressure Variations," Twenty-Third
Symposium (International) on Combustion, Combustion
Institute, Pittsburgh, 1990, pp. 333-340.
2Coward, H., Jones,
C., "Flammability Limits of Gases and Vapors," U. S.
Bureau of Mines Bulletin 503, 1952.
3Ronney, P. D.,
"Effect of Chemistry and Transport Properties on Near-Limit
Flames at Microgravity," Combustion Science and
Technology, Vol. 59, 1988, pp. 123-141.
4Abbud-Madrid, A.
and Ronney, P. D., "Effects of Radiative and Diffusive
Transport Processes on Premixed Flames Near Flammability
Limits," Twenty-Third Symposium (International) on
Combustion, Combustion Institute, Pittsburgh, 1990, pp.
423-431.
5Zeldovich, Ya. B., Theory
of Combustion and Detonation of Gases, Academy of Sciences
(USSR), 1944.
6Ronney, P. D.
"Near-Limit Flame Structures at Low Lewis Number," Combustion
and Flame, Vol. 82, 1990, pp. 1-14.
7Ronney, P. D.,
Whaling, K. N., Abbud-Madrid, A., Gatto, J. L. and Pisowicz, V.
L., "Stationary Premixed Flames in Spherical and Cylindrical
Geometries," AIAA Journal., Vol. 32, 1994, pp.
569-577.
8Buckmaster, J. D.,
Joulin, G. and Ronney, P. D., "Effects of Heat Loss on the
Structure and Stability of Flame Balls," Combustion and
Flame, Vol. 79, 1990, pp. 381-392.
9Buckmaster, J. D.,
Joulin, G. and Ronney, P. D., "Structure and Stability of
Non-adiabatic Flame Balls: II. Effects of far-field losses,"
Combustion and Flame, Vol. 84, 1991, pp. 411-422.
10Lee, C. and
Buckmaster, J. D., "The Structure and Stability of Flame
Balls: a Near-Equidiffusional Flame Analysis," SIAM
Journal on Applied Mathematics, Vol. 51, 1991, pp. 1315-1326.
11Wu, M. S., Ronney,
P. D., Colantonio, R. and VanZandt, D., "Detailed Numerical
Simulation of Flame Ball Structure and Dynamics," to appear
in Combustion and Flame (1998).
12Buckmaster, J. D.
and Joulin, G., "Flame Balls Stabilized by Suspension in
Fluid with a Steady Linear Ambient Velocity Distribution," Journal
of Fluid Mechanics, Vol. 227, 1991, pp. 407-427.
13Wu, M. S. and
Ronney, P. D., Twenty-Seventh Symposium (International) on
Combustion, Combustion Institute, Pittsburgh, 1998, to
appear.
14Lozinski, D.,
Buckmaster, J. D., Ronney, P. D., "Absolute Flammability
Limits and Flame Balls in Optically Thick Mixtures," Combustion
and Flame, Vol. 97, 1994, pp. 301-316.
15Batchelor, G. K., An
Introduction to Fluid Dynamics, Cambridge University Press,
Cambridge, U.K., 1967.
16Buckmaster, J. D.
and Ronney, P. D., "Flame Ball Drift in the Presence of a
Total Diffusive Heat Flux," Twenty-Seventh Symposium
(International) on Combustion, Combustion Institute, 1998, to
appear.
17Frenklach, M., et
al., "An Optimized Kinetics Model for Natural Gas
Combustion," Twenty-Fifth Symposium
(International) on Combustion, Poster 26, Session 3, 1994.
18Peters, N. in: Reduced
Kinetic Mechanisms for Applications in Combustion Systems, N.
Peters and B. Rogg (Eds.), Springer-Verlag, Berlin-Heidelberg,
1993, Chapters 1 and 5.
19Yetter, R. A.,
Dryer, F. L. and Rabitz, H., "A Comprehensive Reaction
Mechanism For Carbon Monoxide/Hydrogen/Oxygen Kinetics," Combustion
Science and Technology, Vol. 79, 1991, pp. 97-128.
20Mauss, F., Peters,
N., Rogg, B. and Williams, F. A., in: Reduced Kinetic
Mechanisms for Applications in Combustion Systems, N. Peters
and B. Rogg (Eds.), Springer-Verlag, Berlin-Heidelberg, 1993,
Chapter 3.
21Abid, M., Wu, M.
S., Liu, J. B., Ronney, P. D., Ueki, M., K. Maruta, K., Kobayashi
, H., Niioka, T. and VanZandt, D. M., "Experimental and
Numerical Study of Flame Ball IR and UV Emissions," to
appear in Combustion and Flame (1998).











