AME 517, Prof. P. Ronney

Midterm Exam Study Guide

October 22, 2009

Format of the exam

The midterm exam will be open book. You may use any reference materials you want, but no laptop computers. The exam will have both analytical/numerical problems and short-answer questions, covering conceptual knowledge.

Material covered

The exam may cover any material through the end Chapter 6. This material includes:

Fundamentals of thermal radiation

Basic laws of thermal radiation

Emissive power, radiative intensity, radiative heat flux

View factors

Definition

Summation rule

Methods for evaluation

Area integration

View factor algebra

Crossed-strings

The inside-sphere and unit sphere

Radiative exchange between diffuse surfaces

Radiative exchange between black surfaces

Radiative exchange between gray, diffuse surfaces

Electrical network analogy

Radiative exchange between partially-specular gray surfaces

Specular view factors

Enclosures with partially-specular surfaces

Radiation shields

Sample midterm (from a previous year)

Problem 1 (physics of radiation) (20 points).

A “two-color pyrometer” is a device that measures the surface temperature of an object assuming it behaves as a gray body (emissivity doesn’t matter as long as it’s independent of wavelength) without needing a reference object. It works by looking at the ratio of intensities at two different wavelengths. For the following measurements, determine the temperature of the test object:

Measurement wavelength 1: 3.5 µm, intensity = 0.504 (units don’t matter)

Measurement wavelength 2: 5 µm, intensity = 1 (in same units as above)

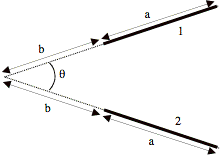
Problem 2 (view factors) (25 points).

For the object shown in the figure:

a) Determine the diffuse view factor F₁₂ as a function of a, b and q.

b) Determine the spectral view factor F₁₁ for the special case q = 45˚, a = √2 – 1, b = 1, r₁^s = r₂^s = 0.5, e₁ = e₂ = 0.5 (think carefully about this problem!)

Problem 2	Problem 3

Problem 3 (Radiative exchange between surfaces) (35 points).

For the configuration shown in the figure above:

a) Calculate the diffuse view factors F₁₂^d and F₂₁^d.

b) Calculate the spectral view factors F₁₁^s, F₁₂^s, F₂₁^s and F₂₂^s if surface 1 is a purely diffuse reflector but surface 2 is a purely specular reflector. Both surfaces are diffuse emitters.

c) Calculate q₁ for the specularly reflecting case, in terms of e₁, T₁, e₂ and T₂ if the surroundings are at 0 K.

Problem 4 (Miscellaneous) (20 points total).

We have discussed the “greenhouse effect” in class, which causes the interior of an enclosure to reach a temperature higher than that of the surrounding air when sunlight passes though a window of the enclosure. Answer and explain briefly the following questions about this effect:

a. Would running a fan inside the enclosure to increase the convective heat transfer coefficient between the interior air and the wall of the enclosure increase or decrease the temperature inside the enclosure?

2. If the window glass absorbed more at short wavelengths than long wavelengths, would the interior of the enclosure warmer, cooler or the same temperature as the outside air?
3. To maximize the greenhouse effect, would you coat the interior of the enclosure with a low emissivity or high emissivity material, or does the emissivity not matter? (Assume whatever coating you use, the emissivity is independent of wavelength.)

Extra problems (not on any previous midterm):

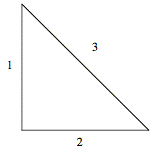
1. For the following 45˚-45˚-90˚ triangular enclosure, surfaces 1 and 2 have a specular component to their reflectivity but surface 2 is a purely diffuse reflector. All surfaces are diffuse emitters. List all 9 specular view factors, F_ij^s (i = 1, 2, 3; j = 1, 2, 3) in terms of the diffuse view factors F_ij^d for these surfaces and their images (for example F_i(j)-i, etc.) and the spectral reflectivities r_i^s. Also draw the images where they exist.

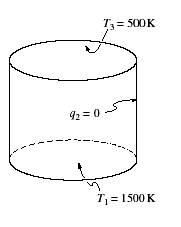
2. a) Determine q₁ for the cylinder shown with diameter 10 cm and length 20 cm. All surfaces are black (e = 1). Also determine T₂.

b) If surface 2 had a heat transfer by convection on its outside surface, with T_∞ = 500K, would T₂ increase or decrease? Would q₁ increase or decrease? (I intentionally didn’t give you a value for h₂; I’m looking for an explanation of what will happen and why).