AME 331, Prof. P. Ronney
Midterm Exam #2 Study Guide
April 17, 2008

Format of the exam

The second midterm exam will be similar to the first midterm - unlimited open book. You may use any reference materials you want.

Material covered

The exam may cover any material through the end of chapter 7 (natural convection) but will emphasize material covered since the first midterm, i.e. convection (chapters 5 – 7, homework sets 4 – 6). This includes:

• Basic fluid mechanical concepts

• Viscosity

• Reynolds and Prandtl number

• Transition to turbulence

• Navier-Stokes equation (F = d(mv)/dt for a fluid)

• Continuity (mass conservation) equation

• Energy equation with convection term

• Forced convection – external flows

• Flow over a flat plate

• Viscous boundary layer

• Thermal boundary layer

• Laminar flow

• Boundary layer thickness

• h and Nu

• Constant surface temperature and constant surface heat flux

• Local vs. averaged h

• Film temperature

• Turbulent flow over a flat plate

• Boundary layer thickness

• h and Nu

• Constant surface temperature and constant surface heat flux

• Cross-flow over a cylinder

• Sphere

• Forced convection – internal flows

• Flow inside pipes

• Entrance vs. fully developed flow

• Friction factor – smooth vs. rough tubes

• Moody diagram

• Bulk temperature (T_b)

• Conservation of energy along the tube length (constant T_w): (T_w – T_b(L))/(T_w – T_b(0)) = exp[(-hπD/C_P)L]

• Hydraulic diameter = 4A/P – use as diameter (D) when no specific relation for the channel shape of interest is available

• Overall heat transfer coefficient (U) – combined effect of convective thermal resistance from the inside fluid to the inside pipe wall, conductive resistances across the wall, convective resistance from the outside pipe wall to ambient fluid outside pipe

• Buoyant (aka natural, free) convection

• Grashof and Rayleigh numbers

• Vertical flat plate

• Constant temperature

• Boundary layer thickness

• d/x = C(Gr_x/4)^-1/4

• d_max, i.e. location where u is maximum: C = -0.25(log₁₀Pr) + 0.9579

• d₉₉, i.e. location where u = 0.01u_max: C = -0.7735(log₁₀Pr)³ + 3.8176(log₁₀Pr)² – 1.1712(log₁₀Pr) + 5.5023

• Constant wall heat flux: use Gr_L^* º gb(q/A)L⁴/kn²

• Horizontal plates

• Horizontal cylinders

• Spheres

• Enclosures

• Summary of convection

• Energy equation has extra term (compared to conduction only) involving fluid velocity

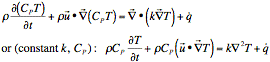
• Need Navier-Stokes equations (x-momentum conservation, y-momentum conservation) plus continuity (mass conservation) for 3 unknowns (x-velocity, y-velocity, pressure) – leads to complicated phenomena (shocks, turbulence, etc.)

• Energy conservation adds one more equation and one more unknown (T)

• To calculate heat transfer coefficient (h), all we really need to know is ∂T/∂y at surface, but in order to get that we have to solve NS + continuity + energy equations!

• At sufficiently high Re or Gr, the effect of viscosity is confined to a thin layer near the surface (boundary layer) which “simplifies” the analysis

• Still, we usually we resort to empirical relations typically of the form Nu = C ReⁿPr^m (forced) or Nu = C RaⁿPr^m (buoyant)

• At least two possibilities to consider

• Surface temperature (T_w) known, calculate surface heat flux (q/A)

• Surface heat flux (q/A) known, calculate surface temperature (T_w)

• Forced convection: free-stream velocity (u_∞) known, calculate entire flow field u(x,y), v(x,y) (u = x-component of velocity, v = y-component of velocity), plug into energy equation

• Buoyant convection: important in most large fluid systems when there is little or no forced flow - complicated interaction between fluid mechanics and heat transfer because momentum and energy equations coupled

• Heat transfer causes DT

• DT causes buoyant force

• Buoyant force causes fluid flow

• Fluid flow causes heat transfer

• Etc., etc.

• Grashof or Rayleigh number describes importance of buoyant flow; generally Gr or Ra ~ Re², where Re is NOT based on u_∞ but rather the velocity induced by buoyancy; frequently (but not always) properties that like Reⁿ in forced flow will scale as Gr^n/2 or Ra^n/2 in buoyant flow

• Be careful – before plugging numbers into a formula, consider

• Forced or buoyant? May need to check both and see which is more important

• Geometry (flat plate, cylinder, enclosure, etc.; if buoyant, horizontal or vertical)

• Laminar or turbulent (depends on Re in forced convection; Gr or Ra in buoyant convection)

• Constant wall temperature or constant heat flux

• Applicable range of Gr or Ra

• Film ( )_f, surface ( )_w, bulk ( )_b or free-stream ( )_∞ temperature – which to use for property evaluation?

• Sometimes problems also include a solid-phase conductivity (e.g. problems involving heat transfer across a pipe wall) but NEVER use the solid-phase conductivity to compute convective heat transfer between the fluid and the solid surface; use solid-phase conductivity to calculate heat transfer across the wall

Note: since empirical relations are important in convection problems, it may be useful to prepare a table with all relevant formulas and their restrictions, or at least Xerox the pages out of the text with the formula summaries. Also be sure you know the definition of Nusselt, Reynolds, Grashof, Rayleigh and Prandtl numbers.

Last year’s second midterm (average 68, high 88)

(Note this was a 55 minute exam because the class met 3 times per week)

Problem #1 (40 points total)

A smooth pipe 1 m long has a constant surface temperature of 90˚C. Water flows into the pipe at 27˚C, that is, T_b(0) = 27˚C. Water properties at 27˚C: r = 997 kg/m³; C_p = 4179 J/kgK; k = 0.613 W/mK; µ = 8.55 x 10^-4 kg/m s; n = 8.58 x 10^-7 m²/s; Pr = 5.83.

(a) (10 points) If the water mass flow rate is 0.01 kg/s and the pipe diameter is 0.03 m, what is the bulk temperature (T_b(L)) at the exit of the pipe?

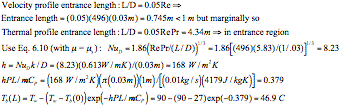
(b) (10 points) If the water mass flow rate is 0.01 kg/s and the pipe diameter is 0.003 m, what is the bulk temperature (T_b(L)) at the exit of the pipe?

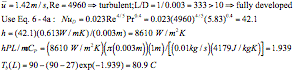
(c) (10 points) If the water mass flow rate is 0.001 kg/s and the pipe diameter is 0.03 m, what is the bulk temperature (T_b(L)) at the exit of the pipe?

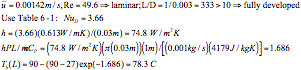
(d) (10 points) If instead the pipe is 1000 m long, for set of conditions, (a), (b) or (c), will the bulk temperature (T_b(L)) at the exit of the pipe be highest? (You don’t have to re-do the calculations in parts (a) – (c), just state your answer and the reason for it.)

With this L, is very large, thus exp(-) ≈ 0, thus T_b(L) ≈ 90˚C for all 3 cases.

Problem #2 (40 points total)

A large covered square pan of warm chili (enough to feed the whole class) is 20 cm tall and has a 40 cm x 40 cm cross-section. The vertical sides and top cover lose heat to the surrounding air at 27˚C by buoyant convection only. The bottom rests on a 60 cm circular disk, which in turn sits on table made of wood (k = 0.25 W/mK) at 27˚C. The pan, cover and disk are made of very conductive steel, so all these surfaces have the same temperature T_s = 50˚C. Air properties at 27˚C: r = 1.161 kg/m³; C_p = 1007 J/kgK; k = 0.0263 W/mK; µ = 1.85 x 10^-5 kg/m··s; n = 1.59 x 10^-5 m²/s; Pr = 0.707.

(a) (15 points) What is the heat transfer coefficient from the vertical sides of the pan to the air?

(b) (15 points) What is the heat transfer coefficient from the top cover of the pan to the air?

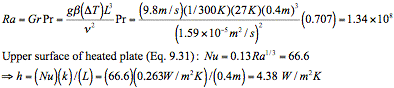
(c) (10 points) What is the total heat loss (in Watts) from the pan, including the top cover, sides and bottom?

Bottom: square with side D to semi-infinite solid; q = kS(DT); S = 2D (Not in your text; I used a different textboox last time.)

q_total = q_top + q_sides + q_bottom = h_topA_topDT + h_sidesA_sidesDT + k_table(2D)(DT)

= (4.38 W/m²K)(0.4 m)(0.4 m)(23K)

+ 4(4.97 W/m²K)(0.2 m)(0.4 m)(23K)

+ (0.25 W/mK)(2)(0.6 m)(23K)

= 59.6 W

Problem #3 (20 points)

Explain the difference between convection heat transfer analyses for constant surface temperature (T_w) vs. constant surface heat flux (q/A). In particular, answer the following questions: (a) Are the governing equations for mass, momentum and energy conservation the same? (b) Are the boundary conditions the same? (c) Are the resulting correlations of Nusselt number to Prandtl and Reynolds (or Grashof) number the same? (d) What is different about the use of relations for constant surface heat flux for buoyant convection than forced convection?

For convection problems, the heat transfer coefficient (h) is defined by the relation q/A = h(DT). Thus, we can consider two cases: one where DT = T_s – T_∞ is known and q/A is computed once we determine h; the other case where q/A is known and DT = T_s – T_∞ is computed once we determine h. Concerning specific questions asked:

(a) Governing equations are exactly the same – mass, momentum and energy still need to be conserved!

(b) Boundary conditions are different:

· Constant surface temperature: T = T_s = constant at y = y_surface

· Constant heat flux: q/A = k_fluid(∂T/∂y) = constant at y = y_surface

(c) No, the resulting correlations Nu = Nu(Re, Pr) or Nu = Nu(Gr, Pr) are different; in the case of forced flow, however, they are ^frequently very similar. For example, for laminar forced flow over a flat plate, Nu_x = 0.332 Re_x^1/2Pr^1/3 for constant T_s and Nu_x = 0.453 Re_x^1/2Pr^1/3 for constant q/A (in this particular case the two correlations are different only by a constant factor of about 1.36; for turbulent flow the difference between constant T_s and constant q/A is even smaller.)

(d) In the case of buoyant convection with q/A = constant we can’t use Gr º gb(DT)x³/n² as the driving force for heat transfer since DT is unknown (DT is what we’re trying to determine). instead we have to use Gr^* º gb(q/A)x⁴/kn² so that we have a quantity using only known parameters. (This was not an issue for forced convection, because in that case the driving force is Re, which doesn’t depend on DT, thus Re can be used in Nu(Re,Pr) correlations for both constant T_s and constant q/A cases.)