AME 331, Prof. P. Ronney
Midterm Exam #1
March 13, 2008

Format of the exam

The first midterm exam will be open book. You may use any reference materials you want. There will be two or three problems similar to the homework problems assigned from the text, appropriately shortened for exam problems. There may also be a short-answer type of question (e.g., define the conduction shape factor, why it is useful and when can it not be used.)

Material covered

The exam may cover any material through the end of chapter 4 (unsteady heat conduction.) This material includes:

• Basic concepts and tools

• Types of heat transfer - conduction, convection, radiation
• Applications
• Governing equation for steady or unsteady conduction
• Buoyancy-driven convection
• Units
• Interpolation
• Engineering scrutiny

• Steady 1-D conduction

•  Planar geometry, constant and variable k
• Thermal resistance
• Radial system
• Critical insulation thickness
• Overall heat transfer coefficient
• Systems with heat sources
• Conduction-convection system (fins)
• Thermal contact resistance

• Steady conduction in multiple dimensions

• Separation of variables
• Rectangular plate
• Conduction shape factors
• Numerical methods

• Unsteady conduction

• Lumped capacity methods
• Semi-infinite solid
• Unsteady conduction with convection boundary conditions - Heisler charts
• Multi-dimensional systems
• Numerical methods

First midterm exam from the last time PDR taught the course (2 years ago)

(Note: some of the Greek symbols don’t show up properly if you’re using a web browser other than Internet Explorer; D = Delta, r = rho, etc.)

Instructions:

55 minutes allowed. Use any non-human reference materials (book, notes, homework, etc.) you want. Be sure to show all your work; liberal partial credit will be given if you have the right idea. Note point values (100 points total) and budget your time accordingly. Make any reasonable assumptions (e.g. steady, constant thermal conductivity, lumped capacity, etc.) you want but be sure to state these assumptions.

Problem #1 (15 points) (Basic concepts)

a. Briefly define thermal resistance

Thermal resistance is analogous to electrical resistance, i.e. the ratio of the driving force for heat transfer (the temperature drop across the thermal element, DT) to the “current” flow of heat transfer (the heat rate, q), thus R_th = DT/q.

b. Explain why it is useful

It is useful because various types of thermal resistances (in particular conductive resistance = Dx/kA, convective resistance = 1/hA and contact resistances) can be combined in series and parallel in the same way as electrical resistors to produce a total thermal resistance R_th,total, and thereby produce an equivalent “circuit” that can be analyzed in a simple way, e.g. q = DT_overall/R_th,total.

c. Explain under what circumstances it is not applicable, or at least is not likely to provide accurate estimates of temperatures and/or heat transfer rates.

• Doesn’t work for multi-dimensional heat transfer since then one can’t create a simple equivalent circuit in the same way that electrical current flows through wires and resistors in a one-dimensional way
• Doesn’t work for unsteady heat transfer (well you could include thermal “capacitors” in your circuit but we didn’t discuss that)
• Doesn’t work when there is heat generation within the material
• Not convenient to use if conductivity is a function of temperature, because then the thermal resistance is a function of temperature.

Problem #2 (30 points) (1D steady conduction)

A solid sphere of uranium has radius r_s and conductivity k, and (via radioactive decay) generates (units Watts/m³) of heat per unit volume. The outer radius of the sphere is maintained at a constant temperature T_s.

a) (10 points) Write down the appropriate governing equation for this system (i.e the equation that ensures conservation of energy + Fourier’s Law is satisfied for this system.)

Assuming constant k,

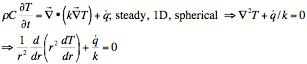
b) (8 points) How many boundary conditions are needed, and what are they?

One 2^nd order ordinary differential equation, requires 2 boundary conditions

(1) Specified temperature at outer radius of sphere: T = T_s at r = r_s

(2) Symmetry condition at r = 0:

c) (12 points) Solve the governing equation with the boundary conditions to determine the temperature profile T(r) inside the sphere in terms of the parameters r_s, k, and T_s.

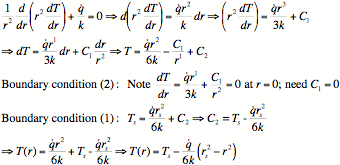
Problem #3 (30 points) (1D unsteady conduction)

A plastic bead 10 mm in diameter having k = 0.2 W/mK initially has a uniform temperature of 350K and is surrounded by air (k = 0.025 W/m˚C) at 300K with convection heat transfer coefficient h = 20 W/m²K. The density (r) and heat capacity (C_P) of the plastic are 200 kg/m³ and 1000 J/kgK, respectively. Assume all properties are independent of temperature. The plastic does not radiate.

a) (15 points) What would the center temperature of the bead be after 50 seconds? Do not use a lumped capacitance analysis.

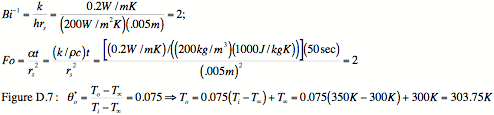
b) (5 points) Could a lumped capacity analysis have been used in this situation? Why or why not?

For the purpose of computing Bi to determine whether the lumped capacity method can be used, the text (p. 245) says to use the definition Bi^* = hL_c/k, where L_c = V/A (V = volume, A = area). For a sphere V = 4πr³/3 and A = 4πr², thus V/A = r/3. Then

Bi^* = (20 W/m²K)(0.005 m/3)/(0.2 W/mK) = 0.17 > 0.1

So NO, lumped capacity method couldn’t have been used anyway.

c) (10 points) How many Joules of heat have been transferred from the bead to the air at this time (50 seconds)?

Bi²Fo = (1/2)² 2 = 0.5; Figure D.9: for Bi²Fo = 0.5, Bi = 0.5, Q/Q_o ≈ 0.9 (it’s hard to tell exactly where Bi = 0.5 since the plot is crazy; it has a logarithmic scale but only 8 lines per decade!)

Q_o = mc(T_i – T_∞) = rVc(T_i – T_∞) = (200 kg/m³)((4π(0.005m)³/3)(1000 J/kgK)(350K – 300K)

= 5.24 J

Q≈ 0.9 Q_o = 4.7 J

Problem #4 (25 points) (2D conduction, numerical methods)

Derive a nodal equation for numerical solution of two-dimensional unsteady heat conduction at a lower right exterior corner node with a constant heat flux per unit area q_laser (from a laser heating source) coming in from the bottom side (no convection on the bottom side), with convection (but no laser heating) on the right side, and having solid thermal conductivity k, density r and heat capacity c. Assume a grid spacing Dx = Dy. Note that the control volume is the diagonal cross-hatched area.

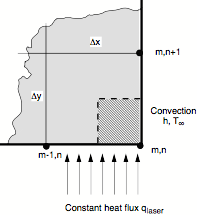
Assuming no heat generation:

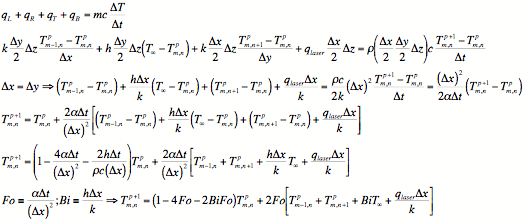
(You don’t need to do all the algebra to get full credit!)